知道油价怎么算加了多少升_怎么用函数算油价

1.基于进出口总量均衡的国际原油价格形成模型

2.count系列5个Excel实用技巧，个个都好用到爆！

3.实证结果分析与讨论

4.国内油价走势曲线是什么?

基于进出口总量均衡的国际原油价格形成模型

4.3.2.1 模型结构

传统经济学商品价格的形成是当该商品的供给等于需求时，市场达到均衡，由此供给（或需求）量所决定的价格就是该商品的均衡价格。通常情况下商品的供给量为产量，需求量为消费量。但由于石油市场受战争、意外的影响较大，战争和意外可能造成石油供应中断，由此对全世界经济生产产生较大的影响。所以现在很多国家都建立了相应的石油储备。由于有存货，当年的消费量不等于当年的石油需求量。同样地，以往的一部分储备有可能转化为供给，因此当年的石油产量也不等于当年的供给量。所以考虑原油市场均衡价格不能直接利用供给（产量）等于需求（消费量）平衡式。如果将国际石油市场看作一个虚拟的商品市场，该市场的流入就是国际石油的总出口，流出就是国际石油的总进口。由于是虚拟市场，因此市场一定会出清，所以每年国际石油市场的总进口等于总出口。

从这个角度来说，可将从国际市场的流出（进口）视为需求（包括当年的消费和储备），将流进（出口）视为供给。国际石油市场出清，意味着进口等于出口，此时国际石油市场达到均衡，由此确定了国际原油价格。在变量的选择上，需求（进口）设定为国际原油价格、世界经济活动水平（实际GDP）和OECD国家石油储备量的函数。供给（出口）方程的因变量为国际原油价格，设国际原油价格为石油出口量、OPEC上期原油产量的函数。当世界经济处于上升时期，各部门扩大生产使得对石油的需求增多，各国增大对石油的进口，即进口量与世界经济活动水平（实际GDP）存在正向变动关系；同样OECD国家增加石油储备需增加石油进口，而减少石油储备，意味着动用一定量的石油储备满足国内需求，这会导致石油进口量的减少，所以OECD石油储备量与国际石油进口量之间也存在着正向变动的关系。对供给方程而言，国际石油出口量越多，表明国际石油市场的石油供给量越多，供给增多，油价走低；反之，国际石油出口量减少，表明供给减少，油价走高。所以国际原油价格与国际石油出口量成反向变动关系。由于OPEC在国际石油市场上的地位，OPEC的产量政策通常作为油价变化的一个指标，增加产量会使油价下跌，减少产量会使油价上升；另外市场对产量变化有一个滞后期，所以OPEC上期原油产量与国际原油当期价格之间存在反向变动关系。

本节石油进出口量数据来自英国石油公司BP网页，世界实际的GDP值来自://genderstats.worldbank.org/query/,OPEC原油产量、国际原油价格和OECD 石油储备量数据来自美国能源网站，时间跨度都是从1989～2003年的年度数据。

4.3.2.2 国际原油价格形成模型

（1）需求函数（表4.4）

表4.4 需求函数表

续表

即

lnIM=0.006lnPC+0.954lnG+0.316lnSO-0.022（4.1）

式中：IM为国际石油进口量；PC为国际原油价格；G为世界实际的GDP; SO为OECD国家石油储备量。

从模型结果来看，所得回归方程的系数符号与前面的分析相一致。世界经济活动水平（实际GDP）对世界石油总出口量（需求）的影响比较显著，其次OECD国家石油储备的变动对石油总出口量的影响也较显著。相比较而言，原油价格变化对石油总需求的影响不显著。这个结论从长期来看是比较合理的，因为石油是一种需求价格弹性较低的商品，其消费量受价格的影响较小。

（2）供给函数（表4.5）

表4.5 供给函数表

即

lnPC=9.077lnEX-10.714lnQO（－1）＋17.276　（4.2）

所得回归方程的系数符号与前面的分析相一致。国际原油价格受到国际石油进口总量和OPEC国家上期产量的显著影响。

（3）市场均衡

IM=EX　　　　　　　　（4.3）

即国际石油市场总出口量等于总进口量，国际石油市场出清，供需达到了平衡。

据此整理得

lnPC=9.147lnG-3.206lnSO-11.326lnQO（－1）－1.14 （4.4）

PC=α·G9.174·SO3.206·QO（-1）-11.326　　　（4.5）

运用上式可以模拟OPEC产量变动对国际原油价格的影响。例如OPEC原油产量减少4%，设世界经济活动水平不变（即值不变），OECD国家需动用约14%的石油储备才能稳定国际原油价格。因为：

PC=0.96-11.326.0.863.206.PC*=PC*

PC*为基准情形时的国际原油价格。

。

类似的，如果世界经济年增长率为3%，在其他因素都不发生变化的情况下，OPEC上期需增加约2.4%的产量，恰好可以稳定国际原油价格。因为：

PC=1.039.174·1.024-11.326·PC*=PC*。

4.3.2.3 修正后的国际原油价格形成模型

随着经济全球化趋势的发展，各国贸易量将越来越大，越来越频繁。石油产品由于其分布的地缘性和主要消费国与主要产油国在地理位置上的分离等特殊性，将使石油产品贸易更依赖于国际市场，所以石油产品贸易量占世界经济（GDP）的份额有增大的趋势。石油产品贸易额占世界GDP的比重越大，国际石油市场越繁荣，这对国际原油价格的产生将起到一定的影响。具体地说，由于国际总进口与总出口相等，所以石油进口开放度增大，意味着石油进口量和出口量同时增加。由于需求和供给同时增加，所以国际原油价格的涨跌由供给和需求的价格弹性确定。供给价格弹性大，原油价格将降低；需求价格弹性大，原油价格将上升。无论何种情况，一般都会影响国际原油价格的形成。下面我们将引入石油进口国开放度概念，进一步研究在进口国开放度变化的情况下各影响因素对国际石油市场的影响。

石油进口国开放度，指国际总的石油进口量与石油出口量的和占世界实际GDP的比例，用TRI表示。即TRI＝（石油总出口＋石油总进口）/世界实际GDP。

考虑石油进口国开放度指标后的石油供给函数如表4.6所示。

表4.6 石油供给函数表

即

lnPC=9.092lnEX-10.727lnQO（-1）＋4.592lnTRI+11.88

所得回归方程中石油进口开放度的系数为正，表明进口开放度增加，国际原油价格将上升。其余变量的系数符号与我们预期的结果一致，即上期OPEC原油产量与当期的原油价格成反比，进口国开放度与国际原油价格成正比。且这3个量对国际原油价格的影响在15%的显著性水平下都是显著的。

在供给函数中引入石油进口国开放度后，拟合指标R-squared和调整的R-squared等各项指标都有所改善，因此引入石油进口国开放度指标有助于更好地拟合原油供给函数。根据市场均衡条件IM=EX，整理得：

PC=α·G9.179·SO3.04·QO（-1）-11.351·TRI4.859　（4.6）

石油进口国开放度的增加表示石油进出口量的增加，反映进口国对石油需求的增加，这在一定程度上可以吸收增加的国际石油产量而保持国际原油价格不变。如：

PC=1.021-11.351·1.054.859·PC*=1.001PC*

count系列5个Excel实用技巧，个个都好用到爆！

哈喽~小可来啦！计数统计，应用的非常广泛~对于不同的实际需求，很多朋友并不知道具体使用哪个计数函数来解决问题！

所以，今天跟大家分享 5 个Excel 常用易学的统计函数 ，让大家能灵活完成统计工作！

1、Count函数

作用： 统计单元格区域或数字数组中数字字段的输入项个数。?

语法： =COUNT(value1,value2,...)?

value1, value2, ... 为包含或引用各种类型数据的参数（1 到 30个），但只有数字类型的数据才被计算。错误值或其他无法转换成数字的文字将被忽略。

在工作中，常常遇到有些表格有项目但无参数，那么如何快速统计这些数据呢？

如下GIF，一键统计有参数的项目：

操作： 输入公式：=COUNT(B2:B12)

说明： 统计B2:B12区域中有参数的项目。

2、Counta函数

作用： 返回参数列表中非空的单元格个数，但其实也可以用来给合并单元格填充序号。

语法： =COUNTA(value1, [value2], ...)

valuel（必需参数）：要计算其中非空单元格的个数的第一项、单元格引用或区域。

value2（可选）：要计算其中非空单元格的个数的其他项、单元格引用或区域，最多可包含255个。

人事工作中会建立人事档案。

但每当增加或减少一名员工时，就需要手动对全体员工重新进行编号，非常浪费时间，怎么解决？

其实 用COUNTA函数为员工添加编号，当人事档案增加或减少员工时，其他员工的编号就自动更新啦！

如下GIF：

操作： 输入公式=COUNTA($B$3:B3)，批量填充。

说明： 对B3单元格引用，确保在复制公式时保持行数不变，因此会始终指向B3的行列数。

3、 Countblank函数

作用：统计指定区域中空单元格的个数。

语法：=Countblank(值或单元格区域)。

有时我们需要在表格中录入大量数据。

埋头苦干之际， 领导突然问还有多少数据没录完 ，还在一个一个的数空白单元格吗？

耗时又易错 ，只需一个COUNTBLANK函数，即可解决这个烦恼。

如下GIF,快速计算数据表内的空白单元格个数:

操作： 输入公式：=COUNTBLANK(A2:A20)。

说明： A2:A20共有8个空的单元格，故公式的统计结果为8。

4、 Countif函数

作用： 统计符合指定单个条件的数量（暨单条件计数）。

语法： =Countif(条件范围，条件)。

在人事工作中， 常 要统计员工出勤状况 ，如：员工正常打卡（以√表示）、请、休息、迟到的次数，咋搞？

如下GIF：

操作： 输入公式：=COUNTIF(A4:J5,K3)，即可算出员工李雪莲的不同出勤状况的次数。

同理， 如下GIF， 也可用来统计“地区”的个数 ：

操作： 输入公式：=COUNTIF(E3:E9,H3)。

说明： 用下拉列表的格式，只需设置一次公式，更具有实用性和通用性呢。

5、 Countifs函数

作用：统计指定条件的单元格格式，可以是多个条件哦（暨多条件计数）。

语法：=Countifs(条件1范围，条件1，条件2范围，条件2……条件N范围，条件N)。

如下GIF，统计指定地区销量大于50的人数：

操作： 输入公式：=COUNTIFS(C3:C9,">="&I3,E3:E9,H3)。

说明：

C3:C9,">="&I3 ?表示C3到C9单元格区域中，大于等于I3单元格的值。

E3:E9,H3 表示E3到E9中等于H3的值。

好啦~今天excel的干货，就分享到这~学完后，大家有没有觉得以上5个函数的用途很大呢？不妨运用到工作中去吧！如果文章对大家有帮助的，建议多多支持鸭！

实证结果分析与讨论

4.4.3.1 WTI和Brent市场收益率的统计特征

令WTI和Brent市场第t日的石油价格分别为P1,t和P2,t，则WTI和Brent市场第t日的对数收益率分别为Y1,t=ln（P1,t/P1,t-1）和Y2,t=ln（P2,t/P2,t-1），从而各得到4943个收益率样本。图4.20是两个市场所有样本收益率的走势图，不难发现，两个收益率序列均存在明显的波动集聚性。

图4.20 WTI和Brent市场原油现货收益率走势

WTI和Brent两个市场样本内收益率的基本统计特征如表4.17所示。总体而言，两个市场的收益率的平均水平和波动水平都非常接近，这也可以从图4.20上得到印证。同时，与标准正态分布的偏度为0、峰度为3相比，本节两个市场收益率的偏度为负（即呈现左偏现象），峰度远大于3，因此它们均具有尖峰厚尾的特征，而且从JB检验的结果也能看到收益率序列显著不服从正态分布。而对收益率序列进行自相关性LB 检验时，根据样本容量，选择滞后阶数为 ，检验结果表明它们均具有显著的自相关性。另外，通过AD F单位根检验，发现它们都是平稳序列。

表4.17 WTI和Brent市场收益率的基本统计特征

4.4.3.2 WTI和Brent市场收益率的GARCH模型估计

（1）WTI市场收益率的GARCH模型估计

为了滤掉收益率序列的自相关性，本节引入ARMA模型对收益率序列建模。根据自相关和偏自相关函数的截尾情况，并按照AIC值最小原则，经过多次尝试，发现ARMA（1,1）模型比较合适。对ARMA（1,1）模型的残差序列进行自相关性Ljung-Box检验，从自相关分析图上看到，残差序列的自相关系数都落入了随机区间，自相关系数的绝对值都小于0.1，与0没有明显差异，表明该残差序列是纯随机的，换言之，ARMA（1,1）模型很好地拟合了原有收益率序列。

鉴于WTI市场收益率序列存在明显的波动集聚性，因此，本节对ARMA（1,1）模型的残差进行ARCH效应检验，结果发现存在高阶ARCH效应，因此考虑用GARCH模型。由于收益率序列存在厚尾现象，因此本节在GARCH 模型中引入GED 分布来描述模型的残差。根据AIC 值最小的原则以及模型系数要显著和不能为负的要求，通过比较GARCH（1,1）,GARCH（1,2），GARCH（2,1）和GARCH（2,2）模型，本节选择GARCH（1,1）模型来拟合原有收益率序列。

为了进一步研究WTI收益率序列的波动特征，本节检验了TGARCH（1,1）和GARCH-M（1,1）模型。结果发现，收益率序列存在显著的TGARCH效应和GARCH-M 效应，即收益率的波动不但具有显著的不对称特征，而且还受到预期风险的显著影响。考虑到模型的AIC值要最小，以及为了描述收益率波动的不对称性，本节选择TGARCH（1,1）模型对WTI市场收益率的波动集聚性建模，模型形式如式4.16。另外，我们看到模型的GED分布参数为1.260823，小于2，从而验证了该收益率序列的尾部比正态分布要厚的特征，也为本节接下来进一步准确计算WTI市场的风险铺垫了良好的基础。

WTI市场收益率的TGARCH（1,1）模型为

国外油气与矿产利用风险评价与决策支持技术

式中：ε1,t-1﹤0,d1,t-1=1；否则，d1,t-1=0;

Log likelihood=11474.52,AIC=-4.898557,GED参数＝1.260823

从模型的方差方程看到，油价收益率下跌时， 对h1,t的影响程度为α1＋Ψ，即0.057202；而油价上涨时，该影响程度为α1，即0.083559，约为前者的1.5倍。h1,t-1前的系数为0.920539，接近1，表明当前方差冲击的92.0539%在下一期仍然存在，因此波动冲击衰减速度较慢，波动集聚现象比较严重。而检验TGARCH（1,1）模型的残差时发现，其自相关函数都在随机区间内，取阶数为68时，残差的Q统计量的显著性概率大于20%，而Q2统计量的显著性概率大于30%，因此经TGARCH（1,1）建模后的序列不再存在自相关现象和波动集聚性。另外，残差的ARCH-LM检验结果也表明，它不再存在波动集聚性，因此TGARCH（1,1）模型对WTI市场收益率序列的拟合效果较好。

（2）Brent市场收益率的GARCH模型估计

基于Brent市场收益率的波动特征，按照与WTI市场GARCH 模型类似的建模思路，建立了MA（1）模型。而利用ARCH-LM检验方法发现模型的残差存在显著的高阶ARCH效应，因此用基于GED分布的GARCH模型。比较GARCH（1,1）,GARCH（1,2）,GARCH（2,1）和GARCH（2,2）模型的AIC值，以及有关系数的显著性，发现选择GARCH（1,1）模型是最合适的，具体形式如（式4.17）。进一步，对收益率序列建立TGARCH（1,1）模型和GARCH-M（1,1）模型，结果表明，有关系数并不显著，因此说明Brent市场收益率的波动并不存在显著的不对称杠杆效应，也不存在显著的GARCH-M效应。而且，我们也发现GED分布的参数小于2，因此验证了Brent市场收益率同样具有厚尾特征。

Brent市场收益率的GARCH（1,1）模型为

国外油气与矿产利用风险评价与决策支持技术

Log likelihood=116.19,AIC=-4.993462,GED参数＝1.324630

在模型的方差方程中，h2,t-1前的系数为0.912673，表示当前方差冲击的91.2673%在下一期仍然存在。可见，与WTI市场类似，Brent市场同样存在波动冲击衰减速度较慢的现象。检验模型的残差，发现其自相关函数都在随机区间内，取阶数为68时，标准残差的Q统计量的显著性概率大于50%，而Q2统计量的显著性概率大于20%，因此经GARCH（1,1）建模后的序列不再存在自相关现象和波动集聚性。另外，残差的ARCH-LM检验结果也表明，它不再存在波动集聚性，因此GARCH（1,1）模型对Brent市场收益率序列的拟合效果也较好。

图4.21给出了两个市场的条件异方差的走势，分别代表着它们的波动水平。从图中看到，一方面，两个市场收益率的波动水平基本相当，只是在某些区间WTI市场的波动会更大一些。当然，在海湾战争期间，Brent市场的波动程度相比而言更剧烈一点；另一方面，两个市场都存在一个明显的现象，那就是在波动比较剧烈的时期，其条件方差最高可达一般水平的20倍以上，这种波动的大规模震荡不但说明了国际石油市场存在显著的极端风险，而且对于市场波动和风险的预测具有重要的现实意义。

图4.21 WTI和Brent市场的条件异方差比较

4.4.3.3 WTI和Brent市场收益率的VaR模型估计和检验

正如前文所述，石油市场需要同时度量收益率下跌和上涨的风险，从而为石油生产者和购者提供决策支持。为此，本节将用上述基于GED分布的TGARCH（1,1）模型和GARCH（1,1）模型，按照方差－协方差方法来分别度量WTI和Brent市场在收益率上涨和下跌时的VaR 风险值。

（1）GED分布的分位数确定

根据GED分布的概率密度函数，使用MATLAB编程，经过多次数值测算，求出GED分布在本节所得自由度下的分位数，如表4.18所示。表中结果显示，95%的分位数与正态分布的1.645基本相同；但99%的分位数却明显大于正态分布的2.326，这也表明了国际油价收益率具有严重的厚尾特征。

表4.18 WTI和Brent市场收益率的GED分布参数及分位数

（2）基于GED-GARCH模型的VaR风险值计算

根据VaR风险的定义，我们得到以下两个计算VaR风险的公式。其中上涨风险的VaR值计算公式为

国外油气与矿产利用风险评价与决策支持技术

式中；zm,α﹥0，表示第m个市场中（T）GARCH（1,1）模型的残差所服从的GED分布的分位数；hm,t为第m个市场的收益率的异方差。

同理，得到下跌风险的VaR值计算公式为

国外油气与矿产利用风险评价与决策支持技术

根据上述两个VaR风险计算公式，本节计算了在95%和99%的置信度下，WTI和Brent市场的上涨风险和下跌风险（表4.19，表4.20）。

表4.19 WTI市场收益率的VaR计算结果

表4.20 Brent市场收益率的VaR计算结果

从表4.19和表4.20的实证结果看到，第一，除95%的置信度下市场收益率上涨风险的LR值略大于临界值外，其他所有LR统计量的值均小于相应的临界值，因此按照Kupiec的返回检验方法，可以认为基于GED分布的TGARCH模型和GARCH模型基本上能够充分估计出两个市场收益率的VaR风险值。从市场收益率与VaR风险值的走势也可以看到这一点（图4.22）。第二，在99%的置信度下，两个市场的VaR 模型对收益率的上涨风险比对收益率的下跌风险的估计精度都更高，这可能是由于收益率分布的左尾比较长，GED分布尚未完全捕捉到所有的厚尾现象。而在95%的置信度下，对下跌风险的估计精度更高。第三，从VaR的均值来看，在相同的置信度下，不管收益率是上涨还是下跌，WTI市场的VaR值都要比Brent市场对应的VaR 风险值大，因此需要更多的风险准备金。当然，从图4.23的VaR 风险走势可以发现，事实上，两个市场的VaR风险基本上相差不大，只是在某些样本区间内，WTI市场的风险会超过Brent市场。

图4.22 99%的置信度下Brent市场的收益率及其VaR风险值

图4.23 99%的置信度下WTI和Brent市场收益率上涨和下跌时的VaR风险值

（3）VaR模型比较

在用GARCH模型计算市场收益率的VaR 风险值时，一般都设模型的残差服从正态分布，从而直接令zm,α等于标准正态分布的分位数。但实际上，石油市场的收益率及其模型残差一般都是非正态分布的，因此得到的VaR 模型往往不够充分。为此，本节以99%的置信度为例，建立了基于正态分布分位数的VaR 模型，计算结果如表4.21所示，并与表4.19和表4.20中VaR模型的有关结果进行比较。

表4.21 基于正态分布分位数的VaR模型计算结果

结果表明，从VaR均值上看，基于正态分布的VaR模型在两个市场、两个方向（即上涨和下跌）上计算得到的VaR风险值均比基于GED分布的VaR 模型的相应结果要靠近零点，这从模型失效次数的比较上也能得到验证。再者，由于表4.21中的失效次数均超过了99%的置信度下临界处的失效次数（约为47），因此此时的计算结果低估了市场的实际风险。

而按照Kupiec的返回检验方法，可看出与99%置信度下的临界值6.64相比，不管是WTI市场还是Brent市场，不管是上涨还是下跌方向，用基于正态分布分位数的VaR模型计算市场风险基本上都不够合理。其中，尽管WTI市场的上涨风险计算结果基本上可以接受，但与表4.19中对应的LR值相比，发现后者更加充分而准确。因此，总体而言，用基于GED分布的VaR模型要比基于正态分布的VaR模型更充分而合适，得到的结果更可取。

当然，在95%的置信度下，基于正态分布和GED分布的VaR模型的LR值几乎一样，都是比较充分的。这是由于它们的分位数几乎是一样的，均为1.645左右。

另外，本节通过计算还发现，如果在建立GARCH模型时设残差服从正态分布，而计算VaR时又选择一般所用的正态分布分位数，则得到的VaR模型不管是哪个市场、哪个方向的风险都将很不充分，而先前很多研究往往就是这么做的。

（4）VaR模型的预测能力

从上述分析中可以看到，基于GED-GARCH的VaR模型能够较好地估计和预测样本内数据。为了更加全面检验这种VaR模型的预测能力，接下来本节以95%的置信度为例，用它来预测样本外数据的VaR风险值，并与样本外的实际收益率数据进行比较。结果发现，在WTI和Brent市场上，落在预测得到的正向VaR和负向VaR之间的实际收益率占整个样本外预测区间所有收益率的比例均为95.76%，接近95%；相应的LR值为0.3409，小于95%置信度下的临界值3.84，因此是可以接受的（图4.24，图4.25）。换言之，根据样本内数据建立的VaR 模型用于预测样本外数据的VaR风险时，其预测能力是可以接受的。另外，为了比较，本节也用了广受好评的H SAF方法建立模型，并预测了样本外数据的VaR风险，但检验却发现其在此处的预测结果并不理想。因为不管是WTI市场还是Brent市场，落在预测得到的正向VaR和负向VaR之间的收益率占整个预测区间所有收益率的比例均为91.92%，离95%较远；相应的LR统计量为4.40，大于临界值，因此应该拒绝原设，即认为在此处用HSAF方法预测市场VaR风险并不妥当。

图4.24 95%的置信度下WTI市场的样本外实际收益率与预测VaR值

图4.25 95%的置信度下Brent市场的样本外实际收益率与预测VaR值

4.4.3.4 WTI与Brent市场风险溢出效应检验

得到WTI和Brent两个市场的收益率上涨和下跌时的VaR风险值之后，本节根据Hong（2003）提出的风险－Granger因果检验方法，构造相应的统计量Q1（M）和Q2（M），并通过MATLAB编程求出统计量的值及其显著性概率，从而检验两个石油市场之间的单向和双向风险溢出效应。计算结果如表4.22所示，其中M分别取10,20和30。

表4.22 WTI与Brent市场风险溢出效应检验结果

从表4.22看到，一方面，在95%和99%的置信度下，不管是上涨风险还是下跌风险，WTI和Brent市场都具有显著的双向Granger因果关系，即两个石油市场之间存在强烈的风险溢出效应；另一方面，为了进一步确定风险溢出的方向，我们从利用单向风险－Granger因果检验的统计量Q1（M）计算得到的结果看到，不管置信度是95%还是99%，不管是上涨风险还是下跌风险，都存在从WTI到Brent市场的风险溢出效应。而若Brent到WTI市场的风险溢出情况稍微复杂，在95%的置信度下，只存在收益率下跌方向的风险溢出，而收益率上涨时并不存在；在99%的置信度下，情况则相反，只存在收益率上涨方向的风险溢出，而不存在下跌方向的风险溢出效应。前者可能是由于95%的置信度下收益率上涨方向的VaR 模型不够充分导致，而99%的置信度下VaR模型是非常充分的，因此后者更为可信。换言之，可以认为在99%的置信度下，不存在从Brent市场到WTI市场的风险溢出效应。

这表示，当市场出现利空消息从而导致油价收益率下跌时，WTI市场的风险状况有助于预测Brent市场的风险，而反之不然。当市场出现利好消息从而导致油价收益率上涨时，两个市场的风险的历史信息均有助于预测彼此未来的市场风险。这对有关和企业的科学决策具有一定的借鉴意义。

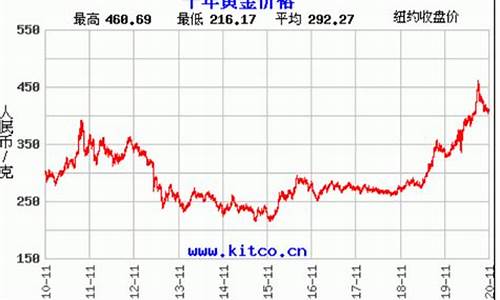
国内油价走势曲线是什么?

国内油价走势曲线是处于一个飞升的状态。作为工业基础原料的石油对于一个国家的经济腾飞具有举足轻重的作用。自从我国加入WTO以后经济发展加速明显，制造业需要大量的石油衍生产品，石油的需求变得越来越大。

油价的趋势

因此研究分析国际油价波动对我国经济可能产生的冲击具有重要意义。传统的石油价格分析多集中在进行一些定性的理论分析或者进行一些比较简单的回归分析，不能清楚地解释说明内部存在的一些统计规律。

本文针对这一状况，把在金融工程中使用较多的ARMA-GARCH理论应用于对油价的分析，并且新定义了一个函数相关度量指标作为研究国内外油价相关程度的一个参考。与以前的定性和回归分析相比，使用ARMA-GARCH以及新的相关度量指标可以更加系统地分析研究油价变动的影响以及波动的趋势。