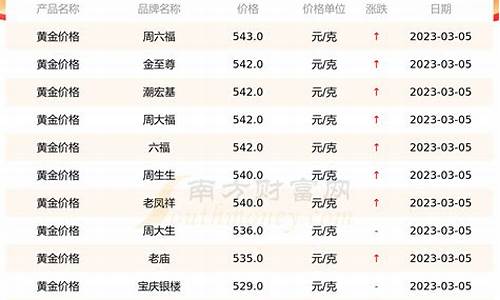
国家油价调价窗口_国家油价调整算法

1.汽车油耗一百公里8.5升 油价是7.1怎么算

2.系统管理

3.我想知道队列算法能干什么

汽车油耗一百公里8.5升 油价是7.1怎么算

油耗的计算为：油耗x油价/100公里。百公里8.5升，按照7块钱一升来算，那么大概需要?60，也就是说每公里六毛钱左右。

假设油箱红灯亮了去加油，加的是92号汽油，单价是6.2元/L，加满后总共用了300块（这里不讲你油箱多少L）。然后你归零公里数，从0公里开始算，等到下次红灯再亮时去加油。此时车子显示你一共跑了 480公里，加了290元，那么我们就得到数据290元跑了480公里。

百公里油耗，就是290元/480公里=0.6 0.6*100=60 60/6.2（油的单价）=9.67L 。

每公里就是290元/480公里=0.6。

每个人的车型不同，性能不同，油耗自然就会不一样，但是算法都是一样的，只要记住初始里程数和结束里程数，就能够算出自己车辆的油耗，但是往往这个实际油耗会比官方给出的油耗要高出一部分。

因为官方给出的数据都是理想状态的，比如一个驾驶员按照一定速度行驶一百公里的油耗，由于多数车辆在90公里/小时接近经济车速，所以大多数官方给出的油耗都是90公里/小时的百公里油耗，这完全就是理想状态。

百度百科-油耗

系统管理

系统的用户包括普通用户和管理员用户两大类。

对于普通用户，系统需要向其提供只读的访问权限，可以查看系统内预定义好的各类风险GIS展示，风险评价指标体系、评价结果，以及不同评价对象的基本信息，另外还可以对系统内的模型运行结果进行查看。

图5.74增加评价方案页面

图5.75修改评价方案页面

图5.76同级指标审核页面

图5.77批量评价页面

管理员用户则需要为系统各模块的正常运行和系统内各种数据的维护等提供支持，系统管理平台的用户对象仅是系统管理员。

系统管理的开发将主要围绕系统管理平台、数据管理和图库管理3方面展开。系统管理平台主要是对整个网站系统的后台管理和网站设置，即实现该原型系统的后台维护。数据管理主要包括油价数据、事件管理，以及基础数据管理。另外，图库管理是针对国家、运输等相关风险中所用到的结构图或地图等进行集中管理。

5.4.5.1系统管理平台开发

以B/S形式运行的风险管理系统的管理平台如图5.78所示。依照数据流程的线索将系统整体功能从左到右进行组织，划分为数据准备、数据处理、数据存储和数据应用四大块，每一块中包括了数据流程不同阶段的具体任务。这些任务以多种形式展现在管理平台界面中，包括中心的流程图形式，左侧菜单和顶层菜单，对系统的管理功能提供了多个访问入口，方便系统管理员对系统功能的把握和调用。

接下来，以主界面中的数据流程图为主线，简单介绍该原型系统的逻辑框架。在系统运行管理平台界面的数据准备中，将系统需要获取的数据分为Internet抽取的价格数据和风险评价数据两大类（见图5.63c）。

在数据处理部分，系统提供对油价数据的进一步整理和数据自动抓取过程中的日志查看，保证系统提供准确完整的数据（见图5.63d）。除此以外，系统管理的数据处理部分包含模型运算模块的调用和管理，以及系统对指标体系和对象评价相关数据的管理。

图5.78系统管理主界面

目前主要介绍的是国家风险、市场风险和运输风险3个子功能模块。此外，除了上面所介绍的系统管理主要框架以外，在系统管理平台中，还添加了系统设置和网站操作模块。系统设置和网站操作主要实现整个原型系统的后台界面框架管理。具体主要包含以下几个方面。

1）直接利用采取Sharepoint列表功能对网站后台框架进行整体设计，可以进行创建、编辑网页、网站框架设计（图5.79）。

图5.79网站操作

2）更改网站主题。网站后台中有多种网站主题，用户可根据需要选择不同的主题（图5.80）。

3）在每一个系统模块下面，可进行整体页面和架构的设计，同时可以编辑相应的超链接条目（图5.81）。

4）在网站设置主页中，高级用户可以进行权限管理，主题外观设置，系统库的管理以及网站集的管理（图5.82）。当然，上述权限操作仅限于高级用户。

5.4.5.2数据管理的开发

数据管理包括油价数据和事件管理、基础数据管理等内容。在油价数据和事件管理中主要完成油价数据和事件的自动抓取功能，基础数据管理将对各个风险模块评价对象的概况、信息等相关数据进行维护和管理。

（1）油价数据和事件管理

油价数据和事件管理的重点是油价和时间数据的获取。系统要求能够实现从Internet中定期自动地抓取数据并存储到系统中心数据库中。

图5.80网站主题更改

图5.81编辑网页

图5.82网站设置

考虑到数据管理和数据库之间的关系比较密切，并且需要不间断地运行，所以对数据管理模块的界面采取了C/S的开发形式。

自动抓取模块的开发内容包括：价格数据抓取算法的设计；事件抓取算法的设计；数据抽取任务控制的整体程序结构确定；任务的自动执行和调度算法的设计；日志功能的使用，要能够依据日志对任务执行中的错误追踪和出错原因进行判断；需要实现任务失败重试，并可以设置重试次数阈值，默认为3次等。

1）调度算法。将抽取代码进行封装，添加调度日志等功能，设计出自动抓取模块流程的整体流程图（图5.83，图5.84）。用于数据管理的管理员界面如图5.85所示。

图5.83自动抓取模块流程图

图5.84自动抓取模块流程图

图5.85数据管理模块界面

2）价格数据抓取算法。自动抓取模块的核心代码是价格数据抓取和事件抓取算法。价格数据抓取从网页中抓取数据存储到本地中来，包括下载模块和处理转换模块两个子模块。自动抓取模块的核心代码部分自动远程下载价格数据，并按照指定路径保存到本地，并将下载结果计人数据库下载日志表，然后将下载下来的Excel表格数据进行转换，转换成符合数据库所建立的表格形式。

对美国能源部的数据抓取代码流程和表格处理转换流程如图5.86与图5.87所示。

图5.86数据抓取代码流程图

图5.87表格处理转换流程图

价格数据抓取模块的技术难点主要有：所下载的表格中包含的市场名称可能会发生变动，难以预期，导致匹配失败；Excel表格中产品名称、市场名称、价格类型、货币类型这几个字段是合并在一起的，需要将其分别识别出来；原表格中的日期格式直接导入数据库会发生不一致现象，需要对其进行转换处理。这些难点的解决主要依赖与算法的设计，在此不再赘述。

3）事件数据抓取算法。事件数据抓取算法要求对美国能源部上关于油品的所有历史事件进行抓取，并保存进数据库。具体实现算法是从美国能源部指定的事件网站上将事件页面的源码下载到本地，然后进行相关字符串抓取、清洗、操作之后进入中心数据库。

事件抓取算法的技术难点，主要在于事件是基于页面HTML形式而非链接，另外抓取的事件要符合数据库规定的形式。解决这些问题的主要方法包括对网页本地化装载的控件进行恰当的选择；在去除页面的HTML标记之后需要附加一些更正性质的处理，比如日期、年份的选择，事件日期、时间和内容之间没有空格的判断问题等；最后，最主要的就是在抓取中大量使用正则表达式提高效率。事件页面的呈现，如图5.88所示。

图5.88国际油价事件

（2）基础数据管理

系统管理平台主要实现基础数据管理。在基础数据管理模块，基于可扩展的数据维护技术，完成了总体架构设计，以国家、运输、市场基础数据为例的基础数据管理功能实现。在基础信息管理下实现了概况、信息、油价、事件等的添加、编辑、修改、更新一系列操作。

在基础数据管理中，实现了国家数据的资源概况、基本信息的页面设计；运输数据的港口、航线概况和基本信息的页面设计；市场数据管理的页面设计，并都实现了链库功能。

图5.63d展示的是系统管理的主界面。其中，最主要的功能是实现基础数据管理操作，该模块仅对高级用户（即有权限进行数据维护的用户）开放。

1）国家数据管理。与风险评价页面相类似，基础数据部分根据模块分了“国家数据”“运输数据”等标签，各标签下又有各自模块的细分功能菜单，显示于页面左侧。国家数据的新增国家和资源概况展示的页面，如图5.89和图5.90所示。

图5.89新增国家页面

图5.90国家基本信息批量展示

2）运输数据管理。运输数据管理模块实现了港口概况、港口信息、航线概况、航线信息的页面设计。现仅以港口信息页面展示为例，如图5.91所示。

5.4.5.3图库管理

在整个风险评价系统中，应用了大量来丰富展现评价对象的相关信息。的应用范围包括：国家对象的地理分布示意以及国家的内部行政划分等；港口对象的标志性，可能是港口的照片或者结构图等；以及其他模块所应用到的。

在图库管理部分，目前考虑的有国家和港口的管理。图库的结构如图5.92所示。

图5.91港口信息维护

图5.92图库管理结构图

图5.93是添加的页面。

图5.94是国家对象图库的显示页面，图5.95是一个具体的对象页面，并且可以在此处删除或者修改。

图5.93图库管理－添加

图5.94图库管理－国家对象图库

图5.95图库管理－国家对象具体显示

我想知道队列算法能干什么

队列是一种先进先出的数据结构，由于这一规则的限制，使得队列有区别于栈等别的数据结构。

作为一种常用的数据结构，同栈一样，是有着丰富的现实背景的。以下是几个典型的例子。

[例5-2] 一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(假设出发时油箱是空的).给定两个城市之间的距离D1,汽车油箱的容量C(以升为单位),每升汽油能行驶的距离D2,出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di,每升汽油价格Pi(i=1,2,……N).

计算结果四舍五入至小数点后两位.

如果无法到达目的地,则输出"No Solution".

样例:

INPUT

D1=275.6 C=11.9 D2=27.4 P=2.8 N=2

油站号I

离出发点的距离Di

每升汽油价格Pi

1

102.0

2.9

2

220.0

2.2

OUTPUT

26.95(该数据表示最小费用)

[问题分析]

看到这道题,许多人都马上判断出穷举是不可行的,因为数据都是以实数的形式给出的.但是,不用穷举,有什么方法是更好的呢 递推是另一条常见的思路,但是具体方法不甚明朗.

既然没有现成的思路可循,那么先分析一下问题不失为一个好办法.由于汽车是由始向终单向开的,我们最大的麻烦就是无法预知汽车以后对汽油的需求及油价变动;换句话说,前面所买的多余的油只有开到后面才会被发觉.

提出问题是解决的开始.为了着手解决遇到的困难,取得最优方案,那就必须做到两点,即只为用过的汽油付钱;并且只买最便宜的油.如果在以后的行程中发现先前的某些油是不必要的,或是买贵了,我们就会说:"还不如当初不买."由这一个想法,我们可以得到某种启示:假设我们在每个站都买了足够多的油,然后在行程中逐步发现哪些油是不必要的,以此修改我们先前的购买计划,节省资金;进一步说,如果把在各个站加上的油标记为不同的类别,我们只要在用时用那些最便宜的油并为它们付钱,其余的油要么是太贵,要么是多余的,在最终的计划中会被排除.要注意的是,这里的便宜是对于某一段路程而言的,而不是全程.

[算法设计]由此,我们得到如下算法:从起点起(包括起点),每到一个站都把油箱加满(终点除外);每经过两站之间的距离,都按照从便宜到贵的顺序使用油箱中的油,并计算花费,因为这是在最优方案下不得不用的油;如果当前站的油价低于油箱中仍保存的油价,则说明以前的购买是不够明智的,其效果一定不如购买当前加油站的油,所以,明智的选择是用本站的油代替以前购买的高价油,留待以后使用,由于我们不是真的开车,也没有为备用的油付过钱,因而这样的反悔是可行的;当我们开到终点时,意味着路上的费用已经得到,此时剩余的油就没有用了,可以忽略.

数据结构采用一个队列:存放由便宜到贵的各种油,一个头指针指向当前应当使用的油(最便宜的油),尾指针指向当前可能被替换的油(最贵的油).在一路用一路补充的过程中同步修改数据,求得最优方案.

注意:每到一站都要将油加满,以确保在有解的情况下能走完全程.并假设出发前油箱里装满了比出发点贵的油,将出发点也看成一站,则程序循环执行换油,用油的操作,直到到达终点站为止.

本题的一个难点在于认识到油箱中油的可更换性,在这里,突破现实生活中的思维模式显得十分重要.

[程序清单]

program ex5_2(input,output);

const max=1000;

type recordtype=record price,content:real end;

var i,j,n,point,tail:longint;

content,change,distance2,money,use:real;

price,distance,consume:array[0..max] of real;

oil:array [0..max] of recordtype;

begin

write('Input DI,C,D2,P:'); readln(distance[0],content,distance2,price[0]);

write('Input N:'); readln(n); distance[n+1]:=distance[0];

for i:=1 to n do

begin

write('Input D[',i,'],','P[',i,']:');

readln(distance[i],price[i])

end;

distance[0]:=0;

for i:=n downto 0 do consume[i]:=(distance[i+1]-distance[i])/distance2;

for i:=0 to n do

if consume[i]>content then

begin writeln('No Solution'); halt end;

money:=0; tail:=1; change:=0;

oil[tail].price:=price[0]*2; oil[tail].content:=content;

for i:=0 to n do

begin

point:=tail;

while (point>=1) and (oil[point].price>=price[i]) do

begin

change:=change+oil[point].content;

point:=point-1

end;

tail:=point+1;

oil[tail].price:=price[i];

oil[tail].content:=change;

use:=consume[i]; point:=1;

while (use>1e-6) and (point=oil[point].content

then begin use:=use-oil[point].content;

money:=money+oil[point].content*oil[point].price;

point:=point+1 end

else begin oil[point].content:=oil[point].content-use;

money:=money+use*oil[point].price;

use:=0 end;

for j:=point to tail do oil[j-point+1]:=oil[j];

tail:=tail-point+1;

change:=consume[i]

end;

writeln(money:0:2)

end.

[例5-3] 分油问题:设有大小不等的3个无刻度的油桶,分别能够存满,X,Y,Z公升油(例如X=80,Y=50,Z=30).初始时,第一个油桶盛满油,第二,三个油桶为空.编程寻找一种最少步骤的分油方式,在某一个油桶上分出targ升油(例如targ=40).若找到解,则将分油方法打印出来;否则打印信息"UNABLE"等字样,表示问题无解.

[问题分析] 这是一个利用队列方法解决分油问题的程序.分油过程中,由于油桶上没有刻度,只能将油桶倒满或者倒空.三个油桶盛满油的总量始终等于开始时的第一个油桶盛满的油量.

[算法设计] 分油程序的算法主要是,每次判断当前油桶是不是可以倒出油,以及其他某个油桶是不是可以倒进油.如果满足以上条件,那么当前油桶的油或全部倒出,或将另一油桶倒满,针对两种不同的情况作不同的处理.

程序中使用一个队列Q,记录每次分油时各个油桶的盛油量和倾倒轨迹有关信息,队列中只记录互不相同的盛油状态(各个油桶的盛油量),如果程序列举出倒油过程的所有不同的盛油状态,经考察全部状态后,未能分出TARG升油的情况,就确定这个倒油问题无解.队列Q通过指针front和rear实现倒油过程的控制.

[程序清单]

program ex5_3(input,output);

const maxn=5000;

type stationtype=array[1..3] of integer;

elementtype=record

station:stationtype;

out,into:1..3;

father:integer

end;

queuetype=array [1..maxn] of elementtype;

var current,born:elementtype;

q:queuetype;

full,w,w1:stationtype;

i,j,k,remain,targ,front,rear:integer;

found:boolean;

procedure addQ(var Q:queuetype;var rear:integer; n:integer; x:elementtype);

begin

if rear=n

then begin writeln('Queue full!'); halt end

else begin rear:=rear+1; Q[rear]:=x end

end;

procedure deleteQ(var Q:queuetype;var front:integer;rear,n:integer;var x:elementtype);

begin

if front=rear

then begin writeln('Queue empty!'); halt end

else begin front:=front+1; x:=Q[front] end

end;

function dup(w:stationtype;rear:integer):boolean;

var i:integer;

begin

i:=1;

while (i<=rear) and ((w[1]q[i].station[1]) or

(w[2]q[i].station[2]) or (w[3]q[i].station[3])) do i:=i+1;

if i0 then

begin

print(q[k].father);

if k>1 then write(q[k].out, ' TO ',q[k].into,' ')

else write(' ':8);

for i:=1 to 3 do write(q[k].station[i]:5);

writeln

end

end;

begin {Main program}

writeln('1: ','2: ','3: ','targ');

readln(full[1],full[2],full[3],targ);

found:=false;

front:=0; rear:=1;

q[1].station[1]:=full[1];

q[1].station[2]:=0;

q[1].station[3]:=0;

q[1].father:=0;

while (front begin

deleteQ(q,front,rear,maxn,current);

w:=current.station;

for i:=1 to 3 do

for j:=1 to 3 do

if (ij) and (w[i]>0) and (w[j]remain

then begin w1[j]:=full[j]; w1[i]:=w[i]-remain end

else begin w1[i]:=0; w1[j]:=w[j]+w[i] end;

if not(dup(w1,rear)) then

begin

born.station:=w1;

born.out:=i;

born.into:=j;

born.father:=front;

addQ(q,rear,maxn,born);

for k:=1 to 3 do

if w1[k]=targ then found:=true

end

end

end;

if not(found)

then writeln('Unable!')

else print(rear)

end.